Research highlights

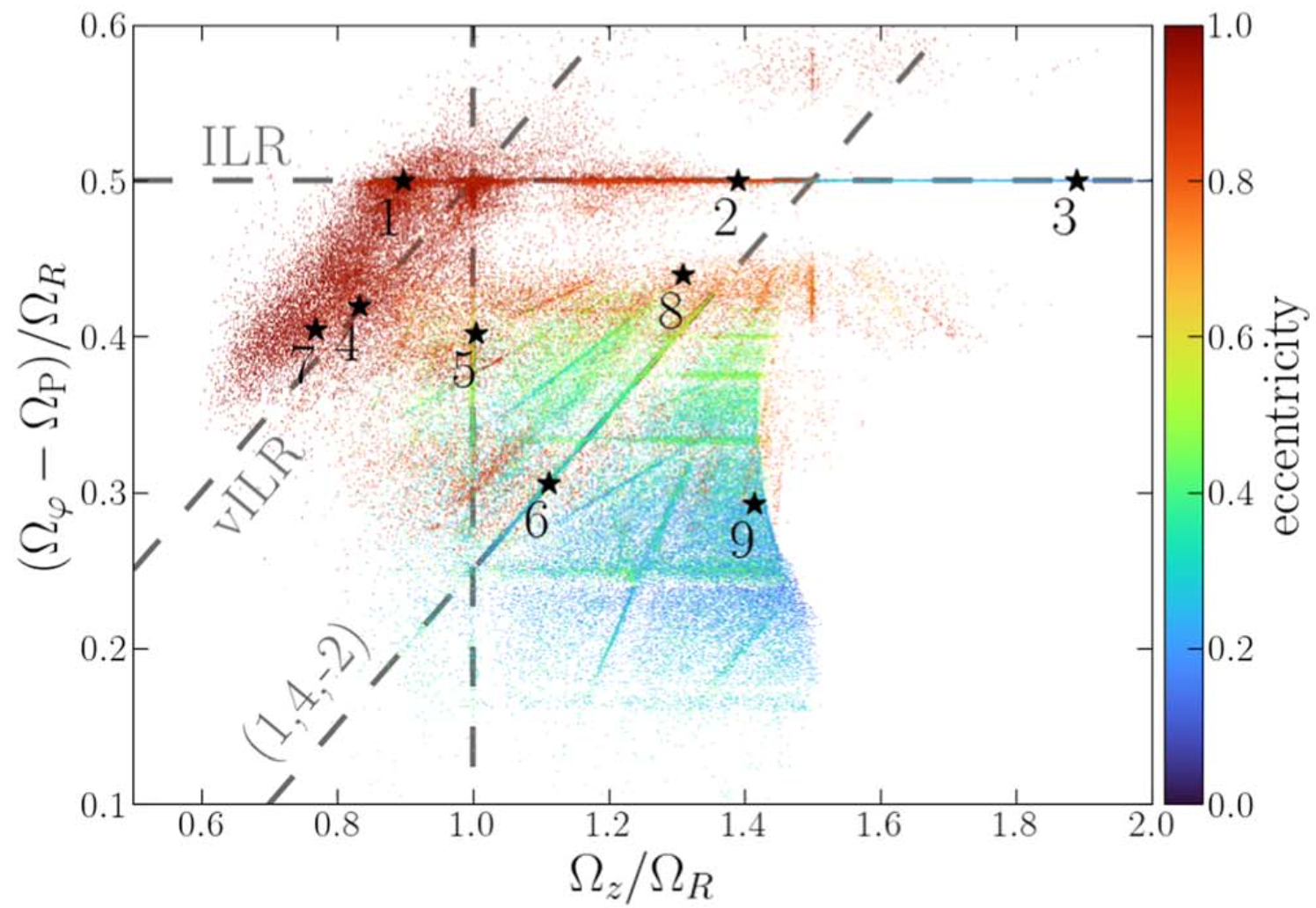Orbital Support and Evolution of Flat Profiles of Bars (Shoulders).
Where we show the important role of resonances in shaping features in galactic bars, in the transition between their flat parts and box-peanut bulges.

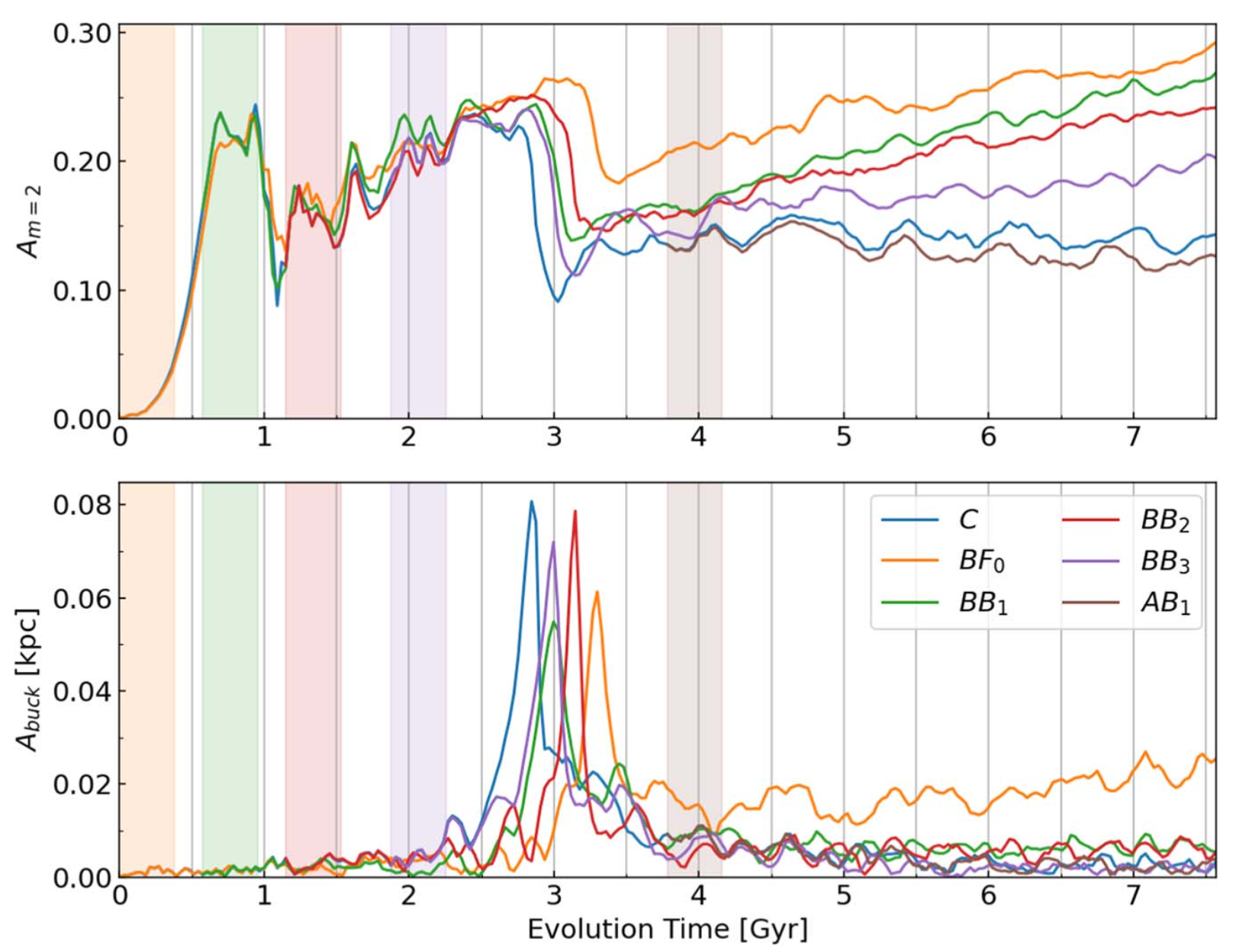Early-growing Supermassive Black Holes Strengthen Bars and Boxy/Peanut Bulges.
Where we show that galactic bars can grow and be stable around black holes.

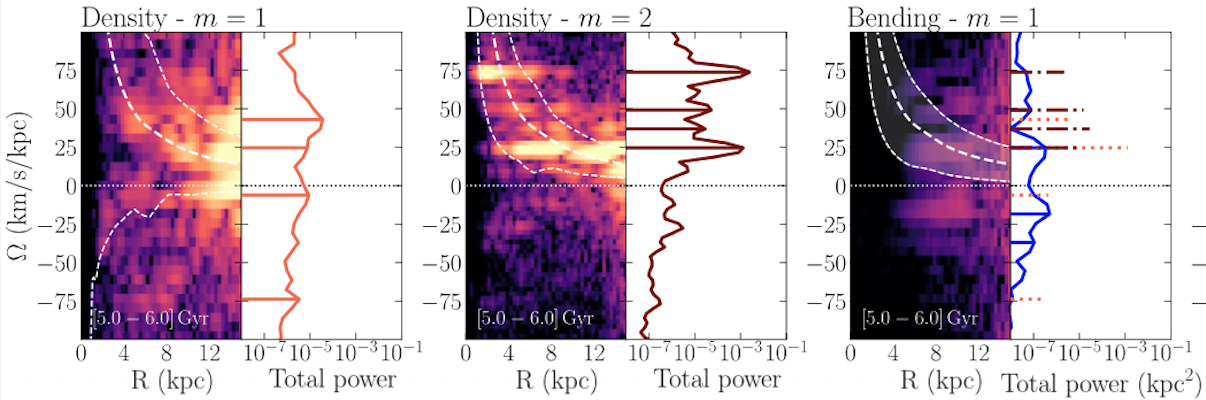Bending waves excited by irregular gas inflow along warps.
Where we show that prograde bending waves in galactic discs can be produced by misaligned gas accretion, and that this is a possible source of vertical perturbations in the Milky Way disc.

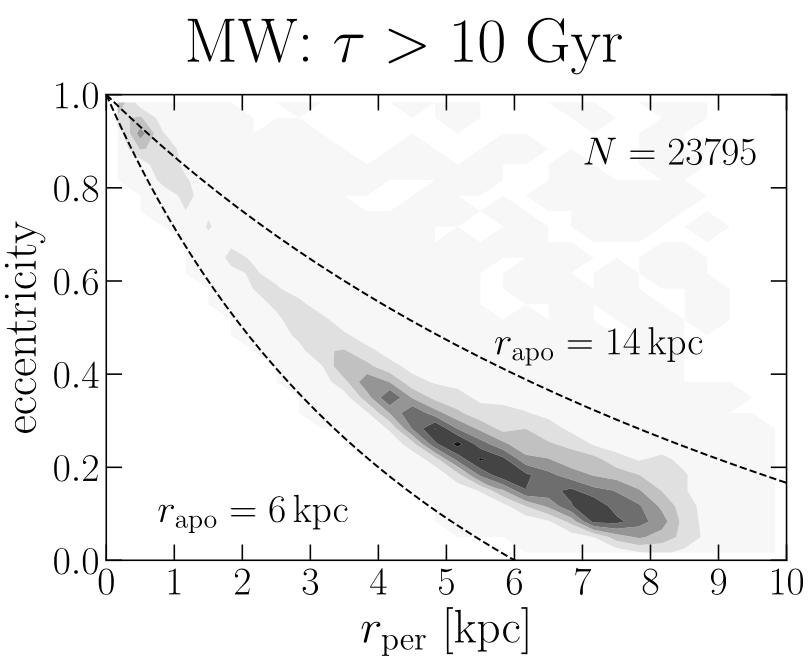Co-formation of the thin and thick discs revealed by APOGEE-DR16 and Gaia-DR2.
Where we find evidence for an old thin disc in the Milky Way, and show that a large population of old stars produce three peaks in the distribution of pericentric distances. The outermost peak ($r_\mathrm{per}\approx 7$ kpc) is produced by radial migration of thin and thick disc stars.

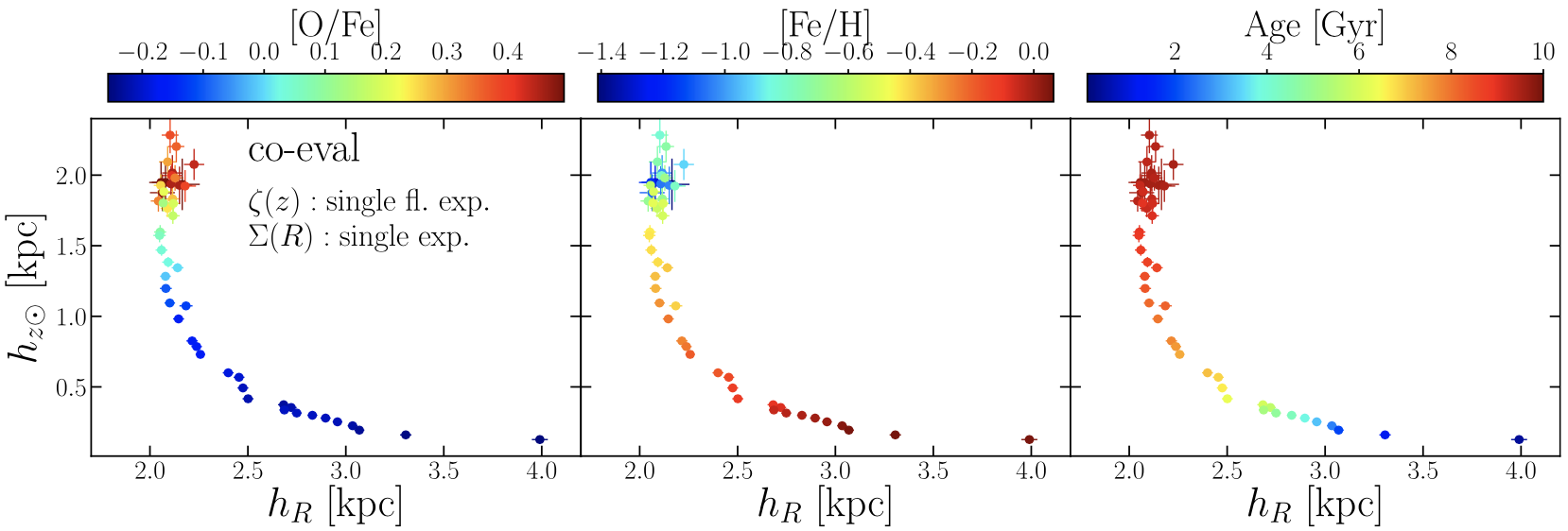Geometric properties of galactic discs with clumpy episodes.
Where we show that galactic discs in simulations with clumps in their early evolution have chemo-spatial trends that agree in detail with those of the Milky Way. In particular, clumps provide a viable scenario for the formation of the thick disc.

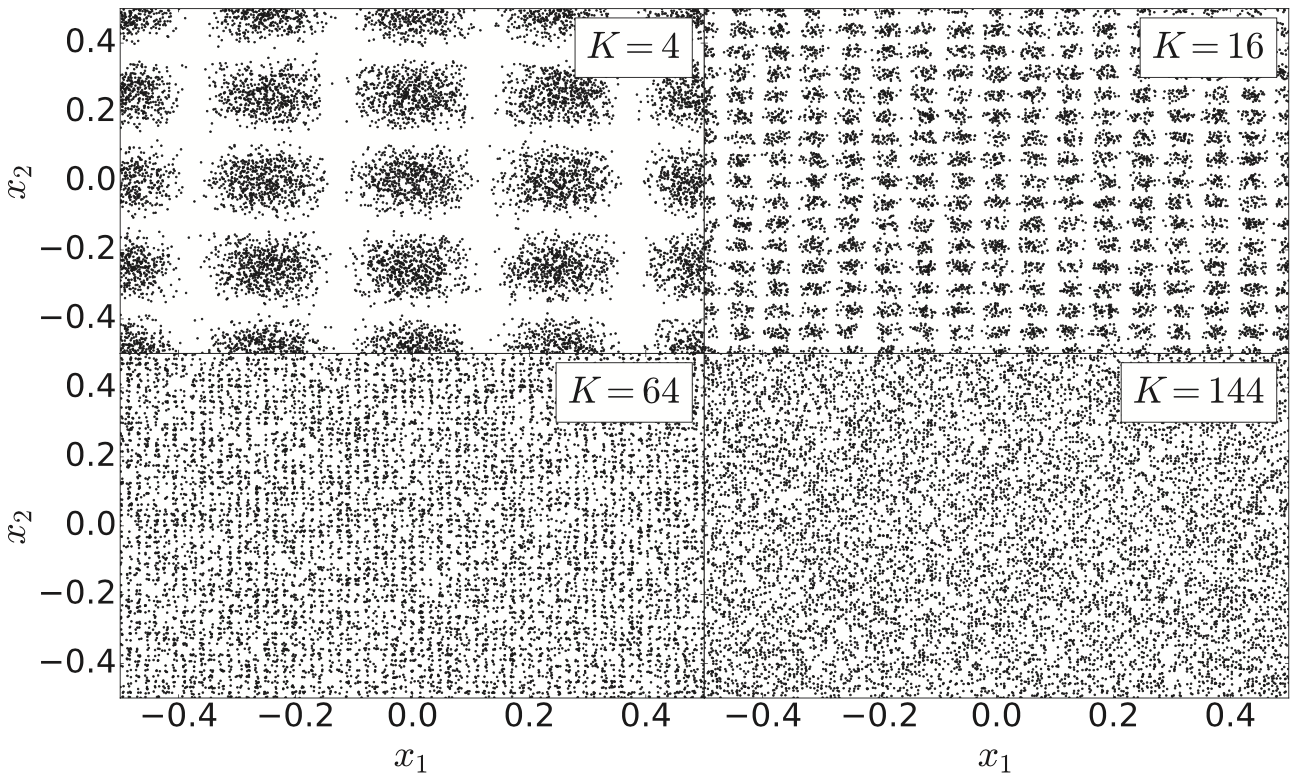The Discreteness-driven Relaxation of Collisionless Gravitating Systems: Entropy Evolution and the Nyquist-Shannon Theorem.
Where we show that the collisionless relexation time $\propto N^{1/6}$ (see below) is a consequence of the Nyquist-Shannon theorem for a 6D phase-space. A finite-$N$ system can develop fine phase-space structures up to a certain limit, but not smaller.

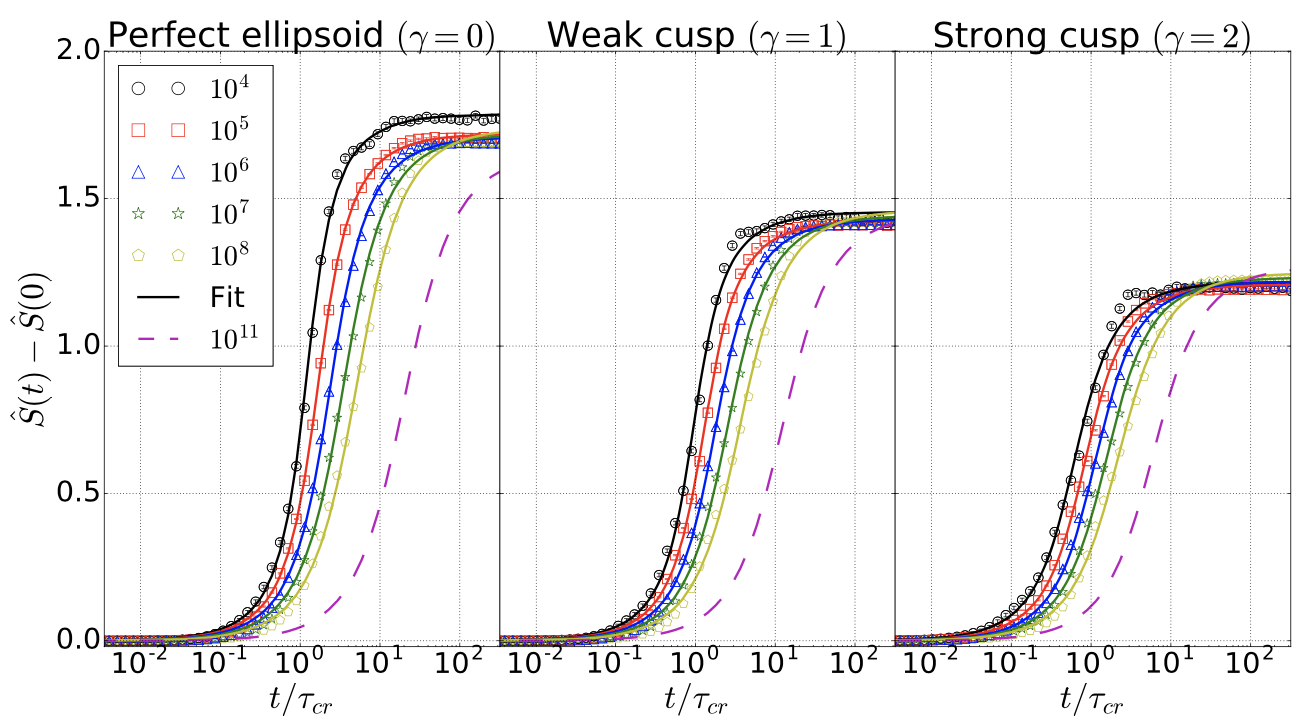The Discreteness-driven Relaxation of Collisionless Gravitating Systems: Entropy Evolution in External Potentials, N-dependence, and the Role of Chaos.
Where we investigate the macroscopic evolution of orbit ensembles in integrable and non-integrable potentials. In contrast to Vlasov eq.'s prediction, the entropy increases quickly, even in integrable potentials. Chaotic motion accelerates the evolution. The collisionless relaxation time is $\propto N^{1/6}$ or shorter.

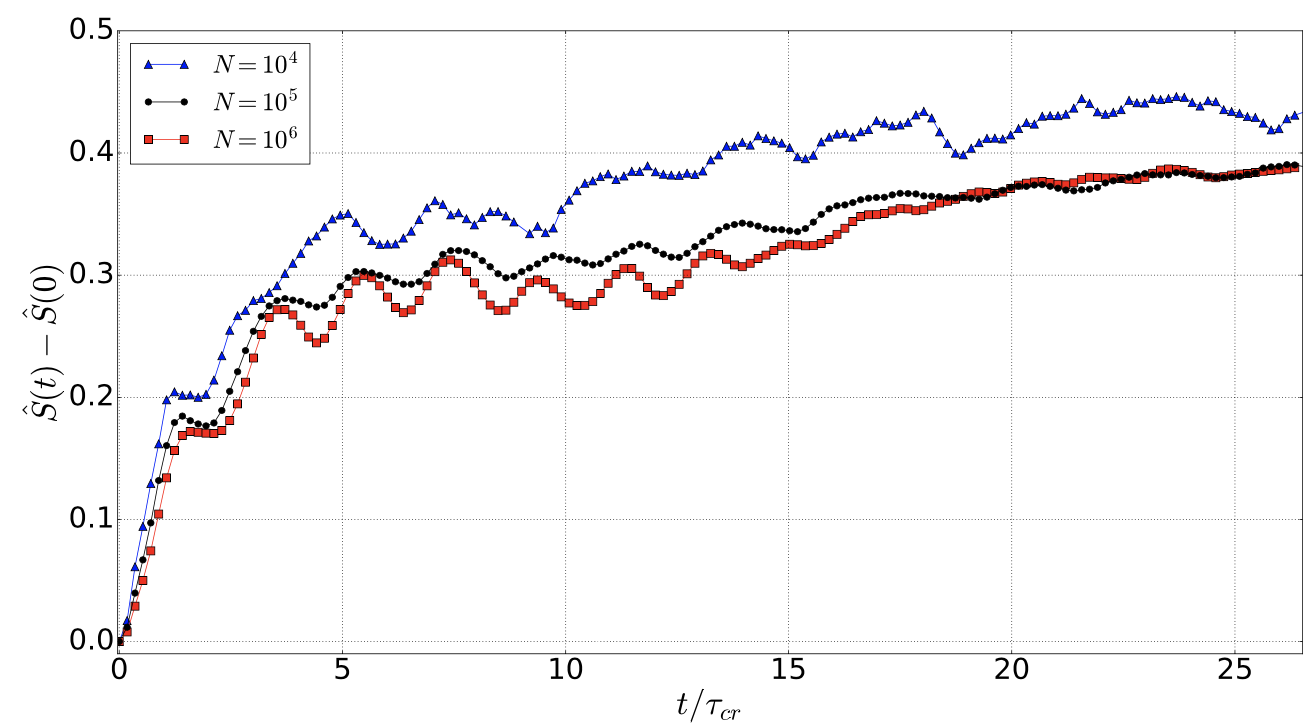The Arrow of Time in the Collapse of Collisionless Self-gravitating Systems: Non-validity of the Vlasov-Poisson Equation during Violent Relaxation.
Where we investigate the macroscopic evolution of self-gravitating systems with entropy estimators in N-body simulations of different numbers of particles. In contrast to Vlasov eq.'s prediction, the entropy increases quickly. The N-dependence is weak.

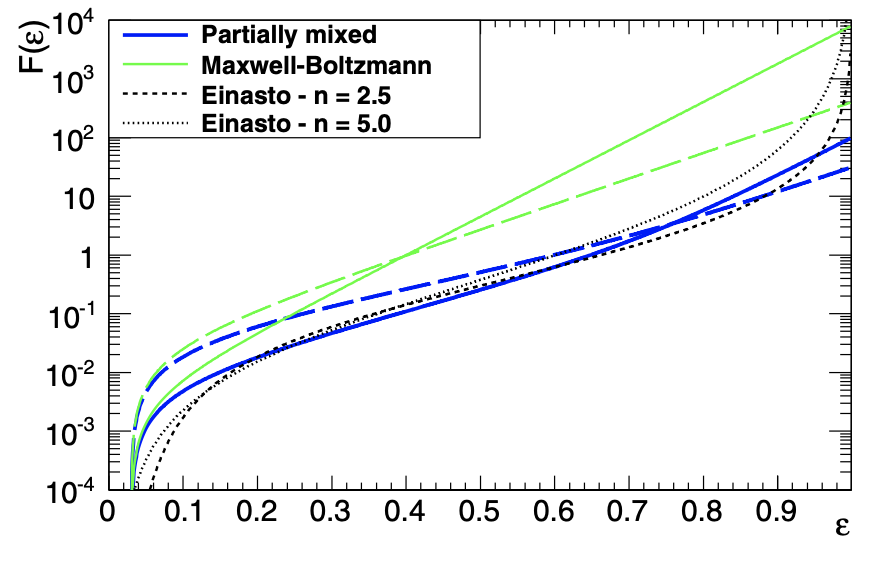Statistical mechanics of self-gravitating systems: Mixing as a criterion for indistinguishability.
Where we associate the mixing level of particles in phase-space to their indistinguishability. This solves the Gibbs paradox without resorting to QM, predicts a more flexible distribution function (plot) and reveals a hidden hypothesis in the derivation of the Vlasov eq. (indistinguishable instead of identical particles).

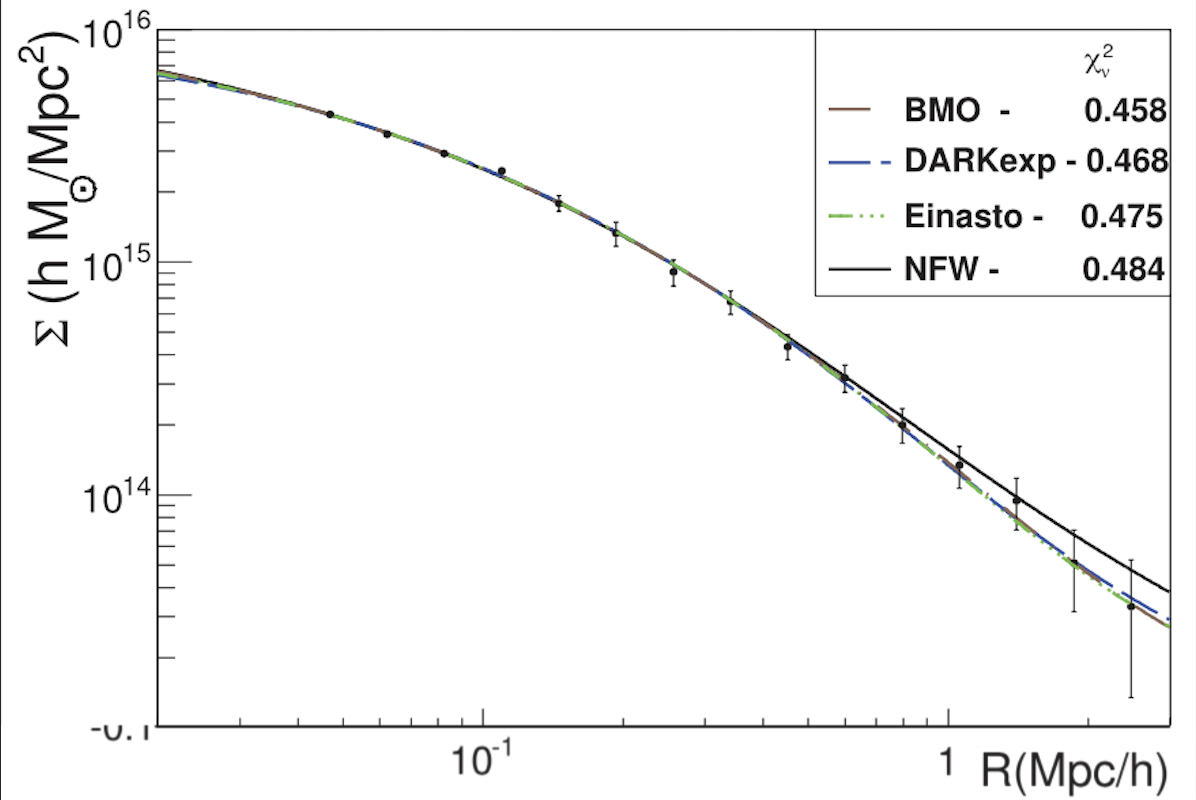Testing phenomenological and theoretical models of dark matter density profiles with galaxy clusters.
Where we show the importance of large-scale (cosmological) contributions in the density profiles of galaxy clusters. With these contributions, the NFW profile overpredicts the density in the outskirts, while steeper profiles like BMO, Einasto and DARKexp provide better fits.